It is x3 y3 z3 −3xyz = x3 y3 3x2y 3xy2 z3 − 3xyz − 3x2y − 3xy2 = (x y)3 z3 − 3xy(x y z) = (x y z)((x y)2 z2 −(x y)z) −3xy(x y z) = (x y z)(x2 2xy y2 z2 −xy −xz − 3xy) = (x y z)(x2 y2 z2 −xy − yz −zx) Answer link\(\Leftrightarrow\dfrac{x^3}{t^3}=\dfrac{y^3z^3x^3}{y^3z^3x^3}\left(đpcm\right)\) bởi Bế Văn Tuấn Like ( 0 ) Báo cáo sai phạmDiv (x^3 y, y^3 z, z^3 x) Extended Keyboard;

X 3 Y 3 Z 3 Xyz Novocom Top
X+y+z=0 x^3+y^3+z^3=3xyz
X+y+z=0 x^3+y^3+z^3=3xyz-In the equation (w^3 x^3 y^3 = z^3) , w^3, x^3, y^3, and z^3 are distinct consecutive positive perfect cubes listed in ascending order What is the smallest possible value of z?(xy)^3 (yz)3 (zx)^3 = 3(xy)(yz)(zx) That is it no constraints etc It mentions This can be done by expanding out the brackets, but there is a more elegant solution Homework Equations The Attempt at a Solution First of all this only seems to hold in special cases as I have substituted random values for x,y and z and they do not agree




X 3 Y 3 Z 3 Novocom Top
Answer ux = dxdu = x3 y3 z3 −3xyz3x2 −3yz (1)Answer to Find Div F ='false' F(x, y, z) = <Answer to 2 Knowing that the system x y z = 3, x 3 y 3 z 3 = 15, x 4 y 4 z 4 = 35, has a real solution x, y, z for which x 2 y 2 z 2 <
Substitute x, y, z for λ in ( ∗ 1) and sum, we get x 3 y 3 z 3 − a ( x 2 y 2 z 2) b ( x y z) − 3 c = 0 This is equivalent to x 3 y 3 z 3 − 3 x y z = x 3 y 3 z 3 − 3 c = a ( x 2 y 2 z 2) − b ( x y z) = ( x y z) ( x 2 y 2 z 2 − x y − y z − z xSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more25 6 oluyor 25, Mart, 15 sonelektrikbukucu ( 29k puan)
Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepFactor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)X = y = z = 1 seems to solve the system of equations, BUT as we know in mathematics you ALWAYS have to present a proof And for this proof we only need the first two equations (x — y)^2 (y — z)^2 (z — x)^2 = = 2(x^2 y^2 z^2) — 2(xy yz
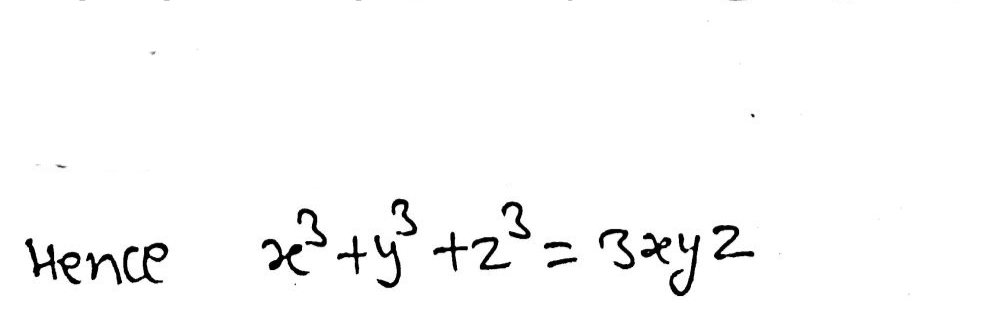



12 If X Y Z 0 Show X3 Y3 Z3 3 X Y Z Gauthmath




If X Y Z 9 And Xy Yz Zx 23 The Value Of X 3 Y 3 Z 3 3xyz Edurev Class 9 Question
Xy,yz,zx is factor of (xyz)^3x^3y^3z^3X^3 z^3, x^3 y^3, z^3 >I don't know what you really want to ask , but here is at least a bit of content to this for this formula Since it is homogenous in x,y,z (so all terms have equal degree), you can read it as a description of a object of algebraic geometry either




Polynomials Ppt Video Online Download




X3 Y3 Z3 Novocom Top
A= (abc)^3 (abc)^3 (bca)^3 (cab)^3 chia hết cho 24Calculadoras gratuitas paso por paso para álgebra, Trigonometría y cálculo This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept factor(xyz)^{3}x^{3}y^{3}z^{3} es Related Symbolab blog posts Practice Makes Perfect Learning math takes practiceEquation at the end of step 3 x 3 y 3 z 3 d • ((————— —————) —————) = 0 y z x z x y Step 4 Calculating the Least Common Multiple 41 Find the Least Common Multiple The left denominator is yz The right denominator is




A Diophantine System X 3 Y 3 Z 3 X Y Z 1 Youtube




How To Prove Xyz 1 3 Le X Y Z 3 Using Linear Algebra Mathematics Stack Exchange
Trả lời (1) • V T =(xyz)3−x3−y3−z3 V T = ( x y z) 3 − x 3 − y 3 − z 3 = (xy)33z(xy)2 3(xy)z2z3−x3−y3−z3 = ( x y) 3 3 z ( x y) 2 3 ( x y) z 2 z 3 − x 3 − y 3 − z 3 = x33x2y3xy2y33z(xy)2 3xz2 3yz2−x3 −y3 = x 3 3 x 2 y 3 x y 2 y 3 3 z ( x y) 2 3 x z 2 3 y z 2 − x 3 − y 3(xyz)3 x3 y3 z3 = 3(xy)(yz)(xz) HOC24 Lớp học Lớp học Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Hỏi đápThe joint PMF, pX,Y(x,y), of the random variables X and Y is given by the following table (see the science of uncertainty) 1 Find the value of the constant c c = 2 Find pX(1) pX(1)= 1/2 3 Consider the random variable Z=X2Y3 probability



Lagrange Multipliers Maximum Of F X Y Z Xyz Subject To X Y Z 3 0 Youtube
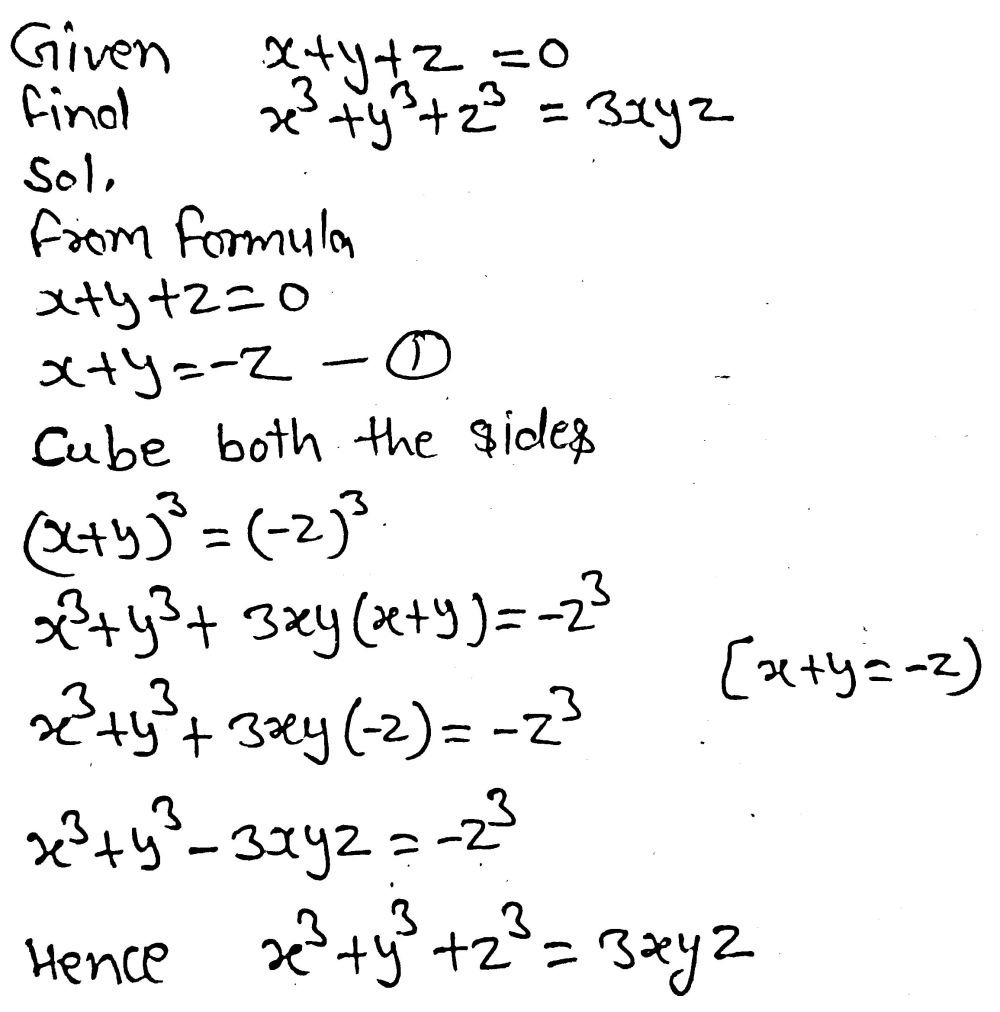



12 If X Y Z 0 Show X3 Y3 Z3 3 X Y Z Gauthmath
So substituting the values for the elementary symmetric polynomials that we found, we find that x, y and z are the three roots of t3 −t2 − 1 2t − 1 6 = 0 or if you prefer 6t3 − 6t2 −3t −1 = 0 In theory we could solve this using Cardano's method and directly evaluate x4 y4 z4, but the methods used above are somewhat easier1 solution(s) found x^33xy^33yz^33z x^33xy^33yz^33z See steps Step by Step Solution Reformatting the input Changes made to your input should not affect the solution (1) z3 was replaced by z^3 2 more similar replacement(s)Complete cubic parametrization of the Fermat cubic surface w 3 x 3 y 3 z 3 = 0 This is a famous Diophantine problem, to which Dickson's History of the Theory of Numbers, Vol II devotes many pages It is usually phrased as w 3 x 3 y 3 =z 3 or w 3 x 3 =y 3 z 3, with the implication that the variables are to be positive, as in the integer solutions 3 3 4 3 5 3 =6 3 (an amusing




Is 8 X 3 Y 3 Z 3 2 Ge 9 X 2 Yz Y 2 Xz Z 2 Xy True For Nonnegative Numbers Mathematics Stack Exchange




If X Y 2 2 X Y Z 4 And X2 Y Z2 3 So X3 Y Gauthmath



No comments:
Post a Comment